20 анимаций, которые объяснят математику простым языком
Для многих математика — это сухие цифры, расчеты и графики, разобраться в которых просто невозможно. На самом деле это совсем не так и вот несколько гифок, которые наглядно показывают те или иные математические законы.
1. Теорема Пифагора:

2. Как понять логарифмы:

3. Лист бумаги, сложенный методом миура-ори:

4. Как на самом деле выглядит число Пи:

5. Визуализация синуса и косинуса:

6. Как площадь круга соотносится с треугольником:

7. Треугольник Рёло — простейшая после круга фигура постоянной ширины. Если к треугольнику Рёло провести пару параллельных опорных прямых, то независимо от выбранного направления расстояние между ними будет постоянным:

8. И с его помощью можно сверлить квадратные отверстия:

9. Как работает треугольник Паскаля (на вершине и по бокам — единицы, каждое число равно сумме чисел, расположенных над ним):

10. Решето Эратосфена — алгоритм нахождения простых чисел до числа n:

11. Шарнирный метод построения лемнискаты Бернулли — алгебраической кривой, похожей на символ бесконечности:
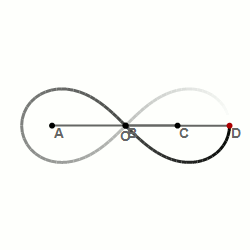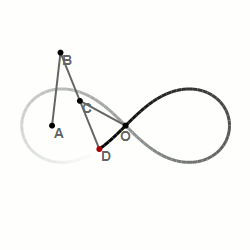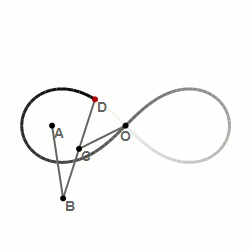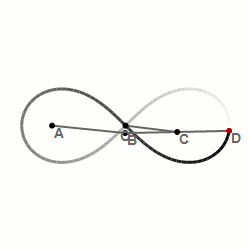
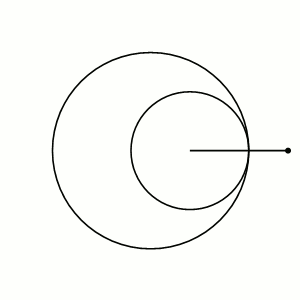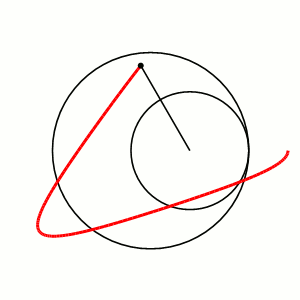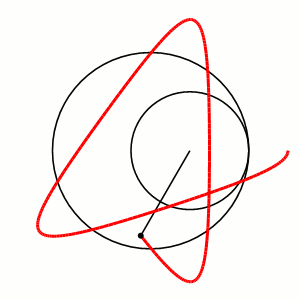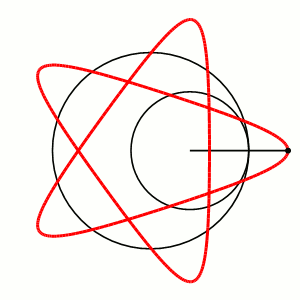
12. Построение гипотрохоиды:
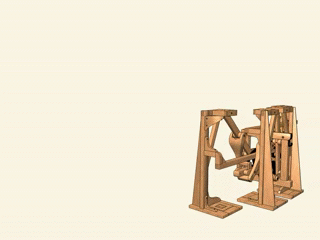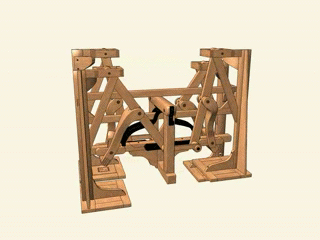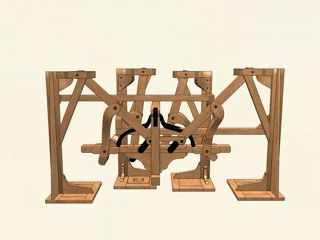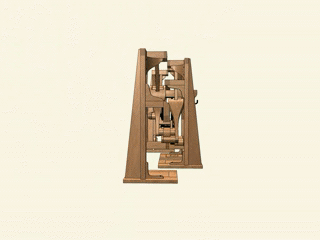
13. Стопходящая машина Чебышева. Да-да, прямо как робот из «Звездных войн»:
14. Так выглядит фрактал:

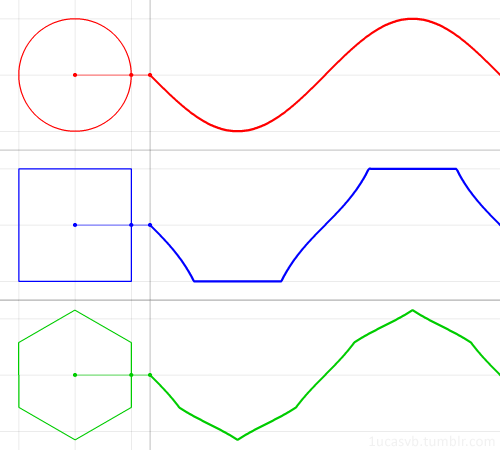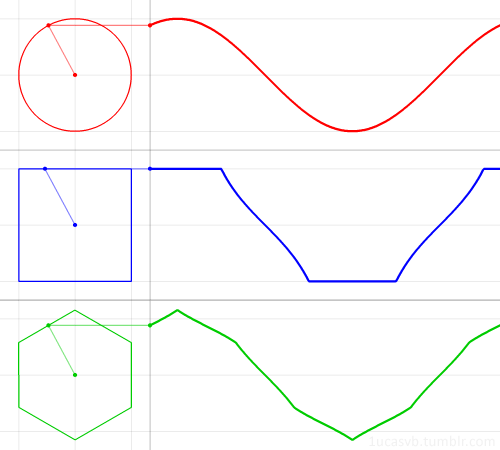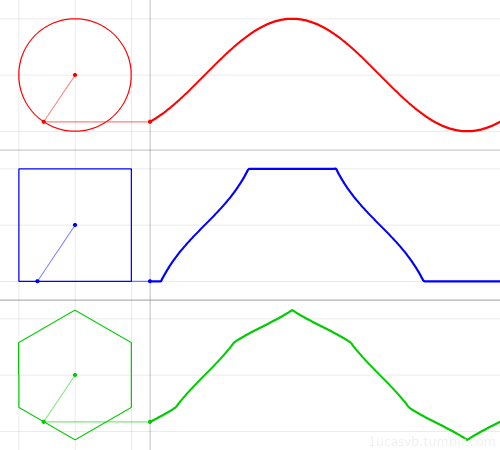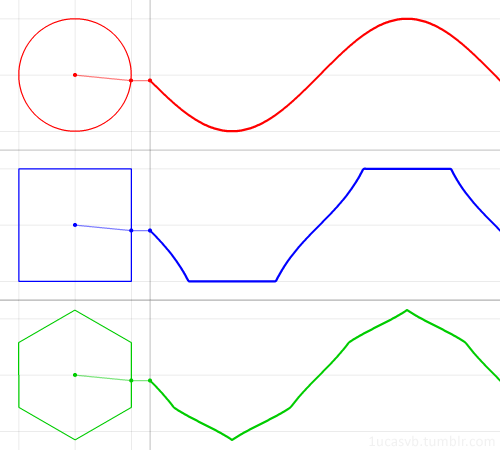
15. Немного построений графиков:
16. Построение треугольника Серпинского с помощью рекурсии:

17. Если вывернуть тор наизнанку, получится еще один:

18. Все углы треугольника могут быть прямыми, если треугольник начерчен на сфере:

19. А так математики шутят:

20. Любите математику!

1. Теорема Пифагора:

2. Как понять логарифмы:

3. Лист бумаги, сложенный методом миура-ори:

4. Как на самом деле выглядит число Пи:

5. Визуализация синуса и косинуса:

6. Как площадь круга соотносится с треугольником:

7. Треугольник Рёло — простейшая после круга фигура постоянной ширины. Если к треугольнику Рёло провести пару параллельных опорных прямых, то независимо от выбранного направления расстояние между ними будет постоянным:

8. И с его помощью можно сверлить квадратные отверстия:

9. Как работает треугольник Паскаля (на вершине и по бокам — единицы, каждое число равно сумме чисел, расположенных над ним):

10. Решето Эратосфена — алгоритм нахождения простых чисел до числа n:

11. Шарнирный метод построения лемнискаты Бернулли — алгебраической кривой, похожей на символ бесконечности:
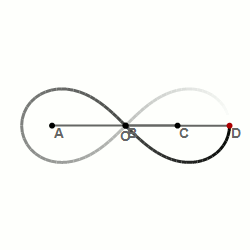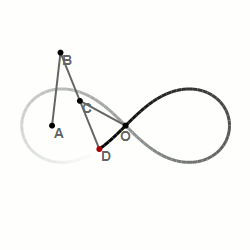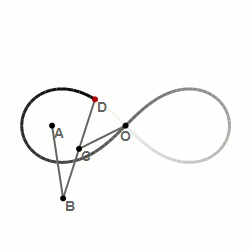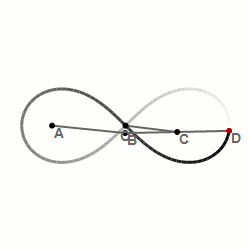
12. Построение гипотрохоиды:

13. Стопходящая машина Чебышева. Да-да, прямо как робот из «Звездных войн»:

14. Так выглядит фрактал:

15. Немного построений графиков:

16. Построение треугольника Серпинского с помощью рекурсии:

17. Если вывернуть тор наизнанку, получится еще один:

18. Все углы треугольника могут быть прямыми, если треугольник начерчен на сфере:

19. А так математики шутят:

20. Любите математику!

Только зарегистрированные и авторизованные пользователи могут оставлять комментарии.
+2
Обалдеть!
Отлично!
- ↓
0
любите математику класс
- ↓
0
Стопоходящая машина…
- ↓